Công thức tính đường cao trong tam giác đều

Công thức tính đường cao trong tam giác đều – có lời giải là một trong những công thức vô cùng quan trọng trong toàn bộ phần hình học cấp 2. Đây cũng là một trong những công thức góp mặt khá nhiều trong các đề thi nên luôn nằm lòng. của sinh viên. Do đó, hãy cùng gia đình mình giải bài toán khó ngay sau bài viết này nhé!

Tam giác đều

Trong hình học, tam giác đều được định nghĩa như sau: tam giác có 3 cạnh bằng nhau thì 3 góc bằng nhau và bằng 60 độ. Trong đó, nó là một đa giác đều có số cạnh bằng 3 nên được gọi là tam giác đều (hình tam giác là kí hiệu của số 3).

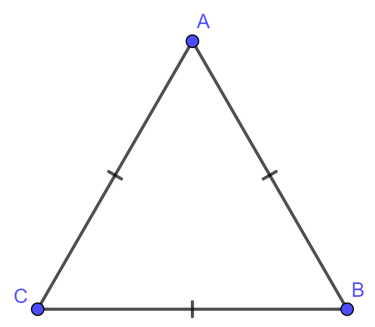
Tính chất của tam giác đều

Một tam giác đều có 5 tính chất như sau:

Trong tam giác đều, mỗi góc bằng 60 độ

Nếu tam giác có 3 góc bằng nhau thì tam giác đó là tam giác đều

Trong tam giác cân có một góc bằng 60 độ là tam giác đều

Trong tam giác đều, đường cao vừa là trung tuyến vừa là tia phân giác của tam giác

+ Giả sử trong tam giác ABC có đường thẳng D xuất phát từ A thì AD vừa là đường cao, trung tuyến, phân giác của góc A.

Đây là 5 tính chất cực kỳ quan trọng trong bài tập hình học, chứng minh hình học, hình học không gian. Các bạn note rõ để áp dụng nhé!

Dấu hiệu nhận biết tam giác đều

Trong 5 tính chất đó có 4 dấu hiệu phân biệt thế nào là một tam giác đều, cụ thể như sau:

Tam giác có 3 cạnh bằng nhau là tam giác đều

Tam giác có 3 góc bằng nhau là tam giác đều

Tam giác cân có một góc bằng 60 độ là tam giác đều

Tam giác có 2 góc bằng 60 độ là tam giác đều

Công thức tính đường cao trong tam giác đều

Có hai công thức tính đường cao trong tam giác đều: tính đường cao của tam giác đều dựa vào công thức Heron và tính đường cao trong tam giác đều dựa vào công thức tính đường cao trong tam giác cân. Cụ thể công thức và cách giải em viết ở phần sau!

Tính độ dài của tam giác đều theo công thức Heron

Công thức được lập nếu công nhận tam giác này là tam giác đều thì độ cao được tính dựa vào công thức Heron như sau:

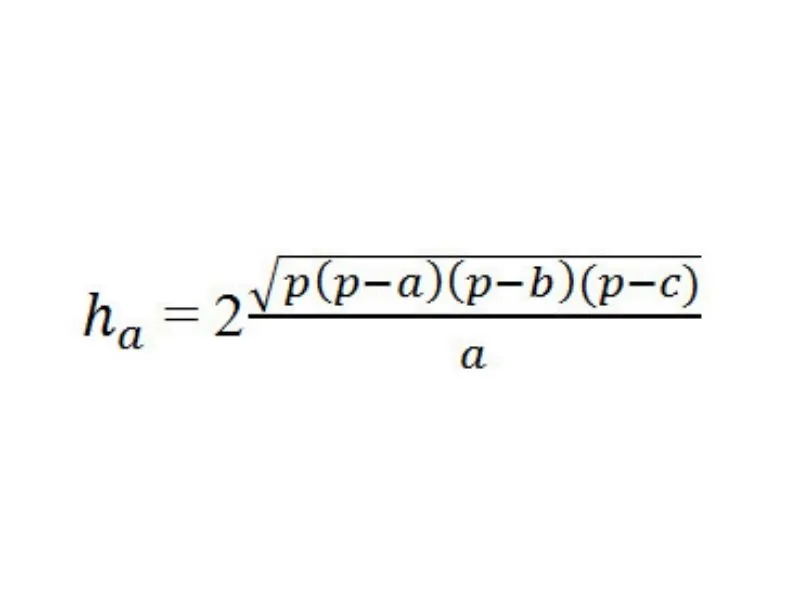
Trong đó:

+ a, b, c gọi là độ dài 3 cạnh của tam giác

+p là nửa chu vi tam giác đều được tính theo công thức sau: p= (a+b+c)/2

+ha là đường cao kẻ từ đỉnh A, h là độ dài chung của 3 đường cao trong một tam giác đều.

Với công thức này, bạn sẽ dễ dàng áp dụng vào các bài tập thực tế trên lớp và các kỳ thi. Mọi người lưu ý lưu lại và ghi nhớ để áp dụng điều Diệc này nhé!

Tính độ cao của tam giác đều dựa vào công thức tam giác cân

Công thức được lập dựa trên công thức tính chiều cao của tam giác cân, độ cao được tính dựa vào công thức cụ thể như sau:

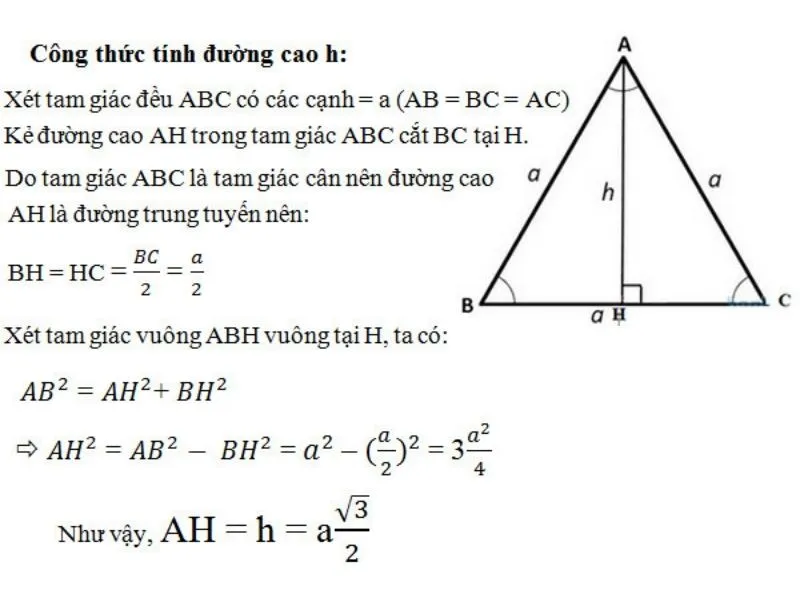
Xét tam giác đều ABC có các cạnh bằng a=AB=AC=BC, có đường cao AH kẻ từ đỉnh A cắt BC tại H. Vì tam giác ABC là tam giác đều nên ABC hiển nhiên là tam giác cân nên đường cao AH cũng là tam giác đều Tam giác. là đường trung bình của ABC. Vậy ta có công thức:

BH = HC = BC/2 = a/2.

Xét tam giác ABH vuông tại H, ta có:

-AB ² = AH ² + BH ² (tính chất của tam giác vuông)

-AH ² = AB ² – BH ² = a ² – (a/2) ² = 3(a ^2/4 )

=> AH = h = (dấu3)/2

Áp dụng công thức tính chiều cao của tam giác đều

Bài toán: Cho tam giác đều ABC có cạnh a=AB=AC=BC= 6. Đường cao AH cắt BC tại H. Tính đường cao AH theo hai cách.

Dung dịch:

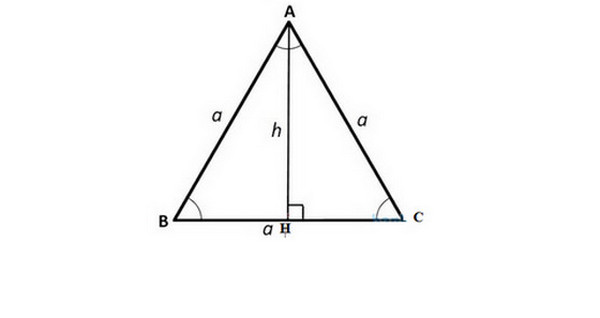
Xét tam giác đều ABC, ta có:

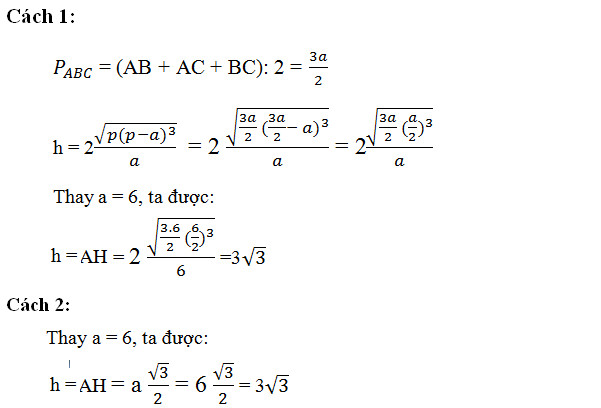
Trên đây là toàn bộ thông tin liên quan đến công thức tính đường cao trong tam giác đều – có lời giải dành cho bạn đọc. Một công thức quan trọng trong nền tảng giải toán hình học. Vì vậy, sau bài viết hi vọng các bạn đã áp dụng công thức vào giải bài của mình. Cảm ơn các bạn đã theo dõi bài viết.